Options and Theta Decay

Anyone trading options would be wise to understand the “Greeks.”

An option’s theoretical value (its premium) is a multivariable function of 5 key variables and is given by the Black-Scholes model (for the classic “European option”).

C(S,T) = S • N(d₁) – K • e^-rT • N (d₂)

d₁ and d₂ are multivariable functions of S, K, T and σ.

S is the spot price – the current underlying stock price.

K is the strike price – the price at which the stock can be exercised.

T is the time to expiration – the remaining time until the option expires.

σ is the implied volatility of the option.

r is the risk-free interest rate.

. . .

That’s all the math you need for options trading.

It’s worth memorizing this formula and its dependencies as it represents many trillions of dollars that are traded on the equities market every day. Specifically, the derivatives market.

The first term S • N(d₁) represents the expected future value of the stock, adjusted by the probability that it will be above the strike price at expiration.

The second term K • e^-rT • N (d₂) discounts the strike price to its present value and adjusts for the probability that the option will not be exercised.

Said another way, an option premium is the expected value based on the two scenarios of the option expiring in-the-money (the first term) and out-the-money (the second term).

. . .

Options Greeks inform traders of their exposure on a position or portfolio basis, can provide valuable insight into risk exposure, and aid with managing risk in portfolios.

Delta (∆), Gamma (Γ), Theta (θ), and Vega (V) are the four major options Greeks traders use. They are in fact “partial derivatives” of the function C(S,T).

1. Delta – direction (bullish/bearish/neutral)
2. Gamma – sensitivity to changes in direction
3. Theta – time value in options prices
4. Vega – sensitivity to changes in volatility
   

Options Greeks can help traders determine their exposure during order entry and understand their options positions’ risk and reward potential.

Investors must consider all four Greeks together to understand the risk and reward potential of an options position during order entry or when analyzing any open options positions.

Options traders must be mindful of the limitations of focusing only on one options Greek, as a trader could overlook information about the risk and reward potential of their options positions.

That’s really all you need to know to be smarter on options trading than 50% of institutional investors. It’s not really that much, but gives you a tremendous edge.

Let’s move onto the focus of this article, which is Theta.

. . .

Theta measures the time value of an option and visually this is what theta looks like.

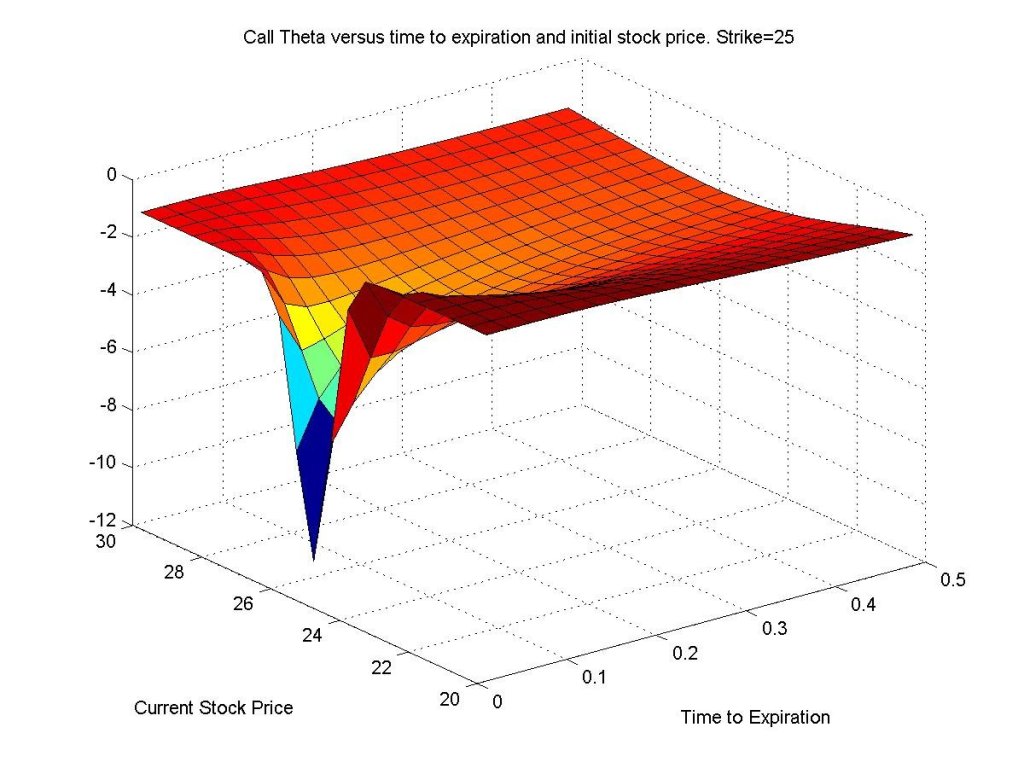
It looks complicated, but let’s break down this graph.

First, remember theta is a partial derivative of the option price with respect to time to maturity or partial ∂C/∂T. It’s simply a mathematical object describing a rate of change.

The graph shows theta at different “times to expiration” (measured in years) and underlying stock price levels (from $20 to $30) for a call option with a strike of $25.

Note how theta is relatively flat for options out-the-money (stock price < $25 strike) and collapses rapidly as one approaches the at-the-money strike of $25.

This precipitous collapse in option price due to time expiration is “theta decay.”

. . .

Why should you care about theta decay?

Well, besides the spot price (delta) and implied volatility (vega), time to expiration (theta) has one of the most important impact on an option price, all else being equal.

Remember, an option price (at a basic Black-Scholes level) is driven by just a few factors.

Two of these factors (the strike and time to expiration), you have 100% control over when purchasing or selling an option.

Let’s take an example from a recent trade idea I covered for NVDA.

The investment thesis is that generative AI will continue to expand due to increased demand caused by DeepSeek’s release and NVDA’s continued monopoly as the sole provider of AI chips for the foundational LLM models like OpenAI and Mistral AI.

Ok, so we want to place a long call option trade.

How should we pick the right option from the NVDA option chain?

First, let’s say we anticipate the market to price in this thesis by the next time NVDA reports their earnings, which will be for FY26 Q1 on 5/28/25.

So we find the first option expiration post that date with enough time for us to say the markets will price in a positive earnings surprise.

Congrats, you are halfway there to being an “event-driven hedge fund manager” – albeit a noobie – but you’re almost there to the big leagues!

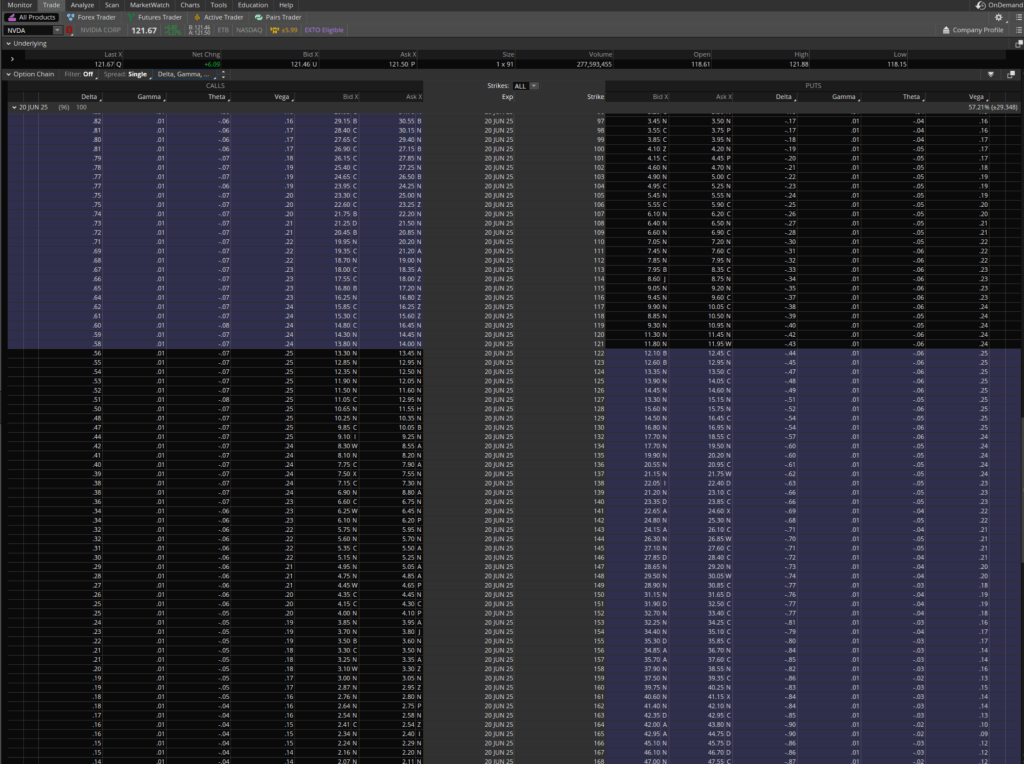
Based on the option chain above, that would be 6/20/25, about a month after Q1 earnings.

So you decided which expiration to buy, now let’s move onto which strike you should buy.

. . .

For determining the optimal strike price, you should be looking at volume, open interest, and underlying human psychology.

Let’s start with the two simpler optimizers which are volume and open interest.

Ideally, you would want a strike that has plenty of liquidity so high volume so you can close the option without having to exercise the contract and being forced to buy the underlying stock (less than ideal).

High open interest is preferably as a well as that indicates there are many contracts that are active and have not settled or closed.

A high volume and low open interest is a red flag as it indicates traders have been closing their contracts, rather than letting it remain open – a bearish indicator.

A low volume and high open interest could be bullish indicator as it may indicate traders are anticipating a higher price movement in the option before expiry.

Here’s what the 6/20/25 expiration looks like for strikes from $100 to $170.

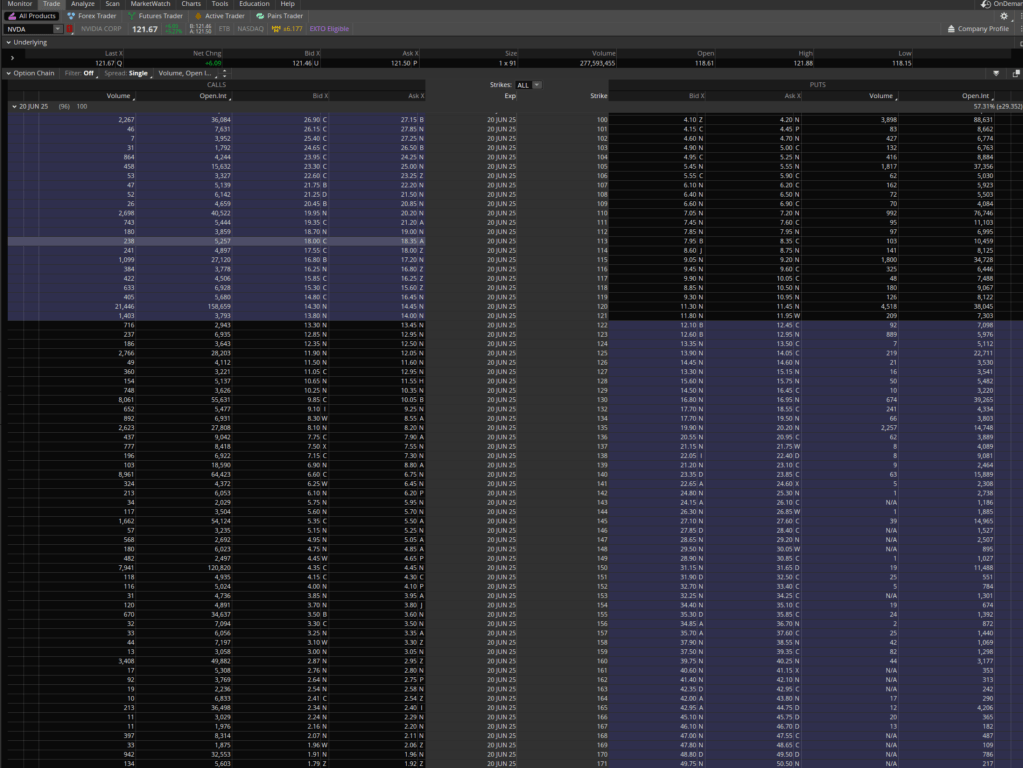
The in-the-money options are highlighted in blue. Generally, if you have a strong conviction on a position (in this case, long NVDA 6/20/25 calls), you should buy the out-the-money options to maximize your leverage and risk-adjusted returns.

In order of open interest from high to low are the $150 strike, $140 strike, and the $160 strike. This makes sense as it appears options traders are implying a positive upside above $150 for NVDA after the FY26 Q1 earnings call.

As we’re truly bullish, you would want to decide between the $150 and $160 strikes.

I’ll let you make that decision based on your risk tolerance, but I think there’s a high probability of NVDA settling above $150 by expiration.

Even if NVDA didn’t settle above $160 by expiration, you can still sell your out-the-money $160 strike for a nice profit before the 6/20/25 expiration (but likely have profits eaten away by theta decay).

I’ll let you decide whether you want to take the red pill ($160 strike) or the blue pill ($150 strike), or maybe even the crazy pill ($200 strike).

So you decided which expiration to buy and which strike to buy (that is, the exact option to purchase), let’s move onto when you should place this event-driven trade.

. . .

This is where it gets a bit technical and where the brief math course I provided earlier comes in handy. Let’s look at the “convexity of theta” – shown as a graph below.

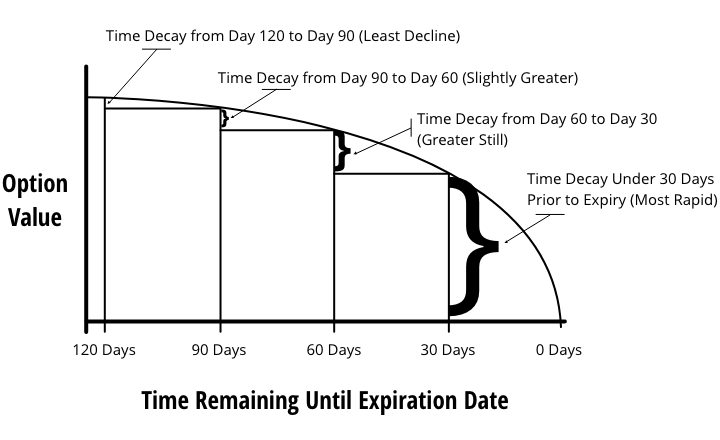
What does it mean that “theta is a negatively convex function for long options”?

It simply means that the closer one gets to expiration, the more rapidly the option price will decline due to time left on expiration.

Thus, you would be ill-advised to buy the 6/20/25 call option with a month left until expiration. Even if there’s a large positive surprise, your option price will rapidly decline in value due to just time.

Time’s role in options – unlike its positive role in time value of money – is reversed here.

Based on the graph, my general heuristic is to place my entry long option trade 60 to 90 days out from expiration. 30 to 60 days is cutting it close. Under 30 days no go.

As of this writing, we’re just 96 days until expiration of the 6/20/25 NVDA calls.

. . .

In case you’re wondering, yes I am an options trader, but more generally a thematic growth investor who leverages options for convexity. I buy and sell stocks and options with the aim of capitalizing and maximizing my risk to reward based upon my theses of high conviction narratives.